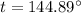Answer:
a)
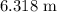
b
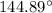
Step-by-step explanation:
Given :
- Length of the aluminium alloy at
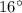
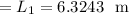
- Length of the aluminium alloy at
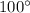
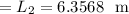
Let
 be the coefficient of linear thermal expansion of aluminium alloy
be the coefficient of linear thermal expansion of aluminium alloy
When the temperate of the rod is increased then its length will be changed accordingly. Let
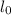 be its length at freezing point of water at T=
be its length at freezing point of water at T=
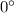
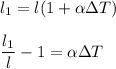
According to question we have
a)
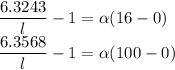
Solving above two equations we get
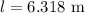
b) Let
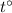 be the temperature of the rod when its length is 6.3689 m then we have
be the temperature of the rod when its length is 6.3689 m then we have
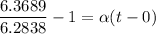
Also we have
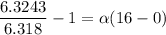
Solving above two equations we have