Step-by-step explanation:
R = Radius of curvature = 20 cm
Focal length = f = R/2 = 20/2 = 10 cm
f = -10 cm (convex mirror)
u = Object distance = 50 cm
Lens Equation
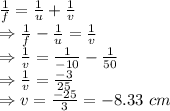
Image is 8.33 cm behind the mirror
As, the sign is negative the image is behind the mirror and is virtual in nature
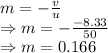
Magnification is 0.166
Positive magnification indicates the image is upright.
R = Radius of curvature = 60 cm
Focal length = f = R/2 = 60/2 = 30 cm
f = -30 cm (convex mirror)
u = Object distance = 200 cm
Lens Equation

Image is 26.08 cm behind the mirror
As, the sign is negative the image is behind the mirror and is virtual in nature
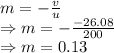
Magnification is 0.13
Positive magnification indicates the image is upright.