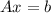Answer:
Explanation:
Let
 be a solution vector of the homogeneous linear system
be a solution vector of the homogeneous linear system
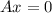 , then,
, then,
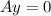 .
.
On the other hand, suppose that
 is a solution vector of the non-homogeneous linear system
is a solution vector of the non-homogeneous linear system
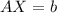 , that is,
, that is,
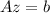 .
.
Now, considering the previous assumptions, you have:
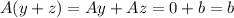
The above demonstrates that the vector
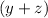 satisfies the system
satisfies the system
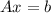 . Then
. Then
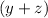 is a solution of the non-homogeneous linear system
is a solution of the non-homogeneous linear system