Answer:
The function is neither injective nor surjective
Explanation:
f: P({1,2,3}) -> N is given by f(A) = |A|
where P(S) denotes the power set of a set S and |A| the number of elements of A
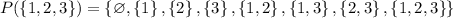
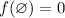
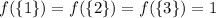


The function is not injective, for
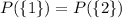
but
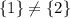
The function is not surjective either, because 5 is a natural number which is not the image of any element A under f, i.e., there is no element in A in P({1,2,3}) such that f(A)=5