Answer:
It will take 4.4 hours to fill the swimming pool when two pumps are opened.
Explanation:
Given:
One pump can fill a swimming pool in 8 hours and another pump can fill it in 10 hours.
First we need to calculate, in 1 hour how much water a pump pour into the swimming pool.
In 1 hour, the first pump can pour water into the swimming pool =
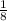
In 1 hour, the second pump can pour water into the swimming pool =
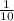
Let "t" be the time taken to fill the pool when two both the pups are opened.
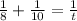
Now we have to solve for t. We have to take LCD of 8 and 10.
The Least common denominator (LCD) of 8 and 10 is 40.
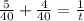
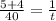
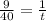
Now we have to cross multiply and solve for t
9t = 40
Dividing both sides by 9, we get
t = 4.444
Which is approximately, t = 4.4 hours.
Therefore, it will take 4.4 hours to fill the swimming pool when two pumps are opened.