Question

A bacteria culture starts with 200 bacteria and grows at a rate proportional to its size. After 6 hours there will be 1200 bacteria (1) Express the population after I hours as a function of t. population: p(tepe (1.066-21) (unction of t) (b) What will be the population after 7 hours? 348125.2 (c) How long will it take for the population to reach 1750 ? Note: You can earn partial credit on this problem.

Answer 1

(1) Let, P represents the size of the bacteria culture in t hours,

According to the question,

`(dP)/(dt)\propto P`

`(dP)/(dt)=kP`

`(dP)/(P)=kdt`

By integrating,

`\ln P=kt + C`

`P=e^(kt+C)`

`P=e^(kt).e^C`

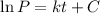
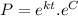
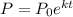`P=P_0 e^(kt)` Where
`e^C=P_0`,

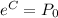We have,

at t = 0, P = 200,

`\implies 200=P_0 e^0\implies P_0 = 200`

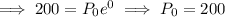
at t = 6, P = 1200

`1200=200 e^(6k)\implies k = 0.299`

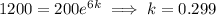
Hence, the required function would be,

`P=200 e^(0.299t)`

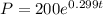
(2) if t = 7,

The population would be,

`P=200 e^(0.299* 7)=1621.84126567\approx 1622`

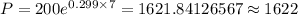
(3) If P = 1750,

`1750=200 e^(0.299t)\implies t = 7.254`

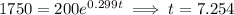
Hence, it will take about 8 years for the population to reach 1750.