Answer: $59313.58
Explanation:
We know that formula we use to find the accumulated amount of the annuity ( ordinary annuity interest is compounded ) is given by :-
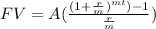 , where A is the annuity payment deposit, r is annual interest rate , t is time in years and n is number of periods.
, where A is the annuity payment deposit, r is annual interest rate , t is time in years and n is number of periods.
Given : Annuity payment deposit :A= $4500
rate of interest :r= 6%=0.06
No. of periods : m= 1 [∵ its annual]
Time : t= 10 years
Now we get,

∴ the accumulated amount of the annuity= $59313.58