Question

Consider the series given below.

2, 6, 18, 54, ...
Given that the sum of the first n terms of the provided series is 6,560, determine the value of n.​

Answer 1

8

Explanation:

Answer 2

n = 8

Explanation:

This is a geometric sequence where the sum to n terms is

`S_(n)` =
`(a(r^n-1))/(r-1)`

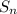where a is the first term and r the common ratio

r = 6 ÷ 2 = 18 ÷ 6 = 54 ÷ 18 = 3 and a = 2, thus

`(2(3^n-1))/(3-1)` = 6560

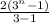`(2(3^n-1))/(2)` = 6560 ← cancel the 2

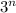`3^(n)` - 1 = 6560 (add 1 to both sides )

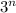`3^(n)` = 6561

note that 6561 =
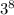`3^(8)`, hence

`3^(n)` =
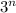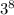`3^(8)` ⇒ n = 8