Question

A person standing on top of a 15-foot high sand pile wishes to estimate the width of the pile. He visually locates two rocks on the ground below at the base of the sand pile. The rocks are on opposite sides of the sand pile, and he and the two rocks are in line with one another. If the angles of depression from the top of the sand pile to each of the rocks are 17 and 25, how far apart are the rocks?

Answer 1

Distance between the rocks = 81.36 feet

Explanation:

In the question,

Height of the person standing on the sand pile from the ground = 15 foot

Angle of depression of a rock on one side = 17°

Angle of depression of other rock on another side = 25°

So,

In the triangles formed, we get,

`tan(25)=(15)/(x)\\x=(15)/(tan(25))\\x=32.18\,foot`

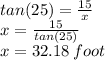
Also,

On the other side of the pile,

`tan(17)=(15)/(y)\\y=(15)/(tan(17))\\y=49.18\,foot`

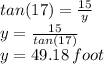
So,

The distance between the rocks is given by = x + y = 32.18 + 49.18

Distance = 81.360 foot