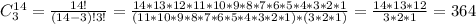Question

involving the election of officers on a committee. Assume that the committee consists of 14 members including Tasha. The same three offices are to be filled. (1) In how many different ways can the offices be filled if each person can hold at most one office?

Answer 1

There are 364 ways of filling the offices.

Explanation:

In this case, the order of filling of the offices does not matter, so, we can figure out the different ways of filling the offices by using the combination formula:

`C^(n) _(r)=(n!)/((n-r)!r!)`

where n=14 (number of members)

r=3 number of offices

n!=n·(n-1)·(n-2)·...·3·2·1

`C^(14) _(3)=(14!)/((14-3)!3!)=(14*13*12*11*10*9*8*7*6*5*4*3*2*1)/((11*10*9*8*7*6*5*4*3*2*1)*(3*2*1))=(14*13*12)/(3*2*1) =364`