Answer:
The velocity at t=1/10s will be:
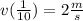
Step-by-step explanation:
The distance in meter as a function of time is:
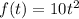 , for 0 ≤ t ≤ 1 where t is in seconds.
, for 0 ≤ t ≤ 1 where t is in seconds.
We need to find the velocity
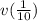 of the surfer at
of the surfer at
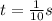 .
.
For this we can use the definition of instantaneus velocity (in it's limit form):
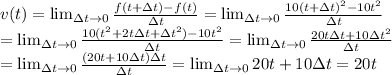
At
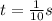 , we have:
, we have:
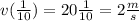 .
.