Question

An optical inspection system is used to distinguish among different part types. The probability of a correct classification of any part is 0.98. Suppose that three parts are inspected and that the classifications are independent. Let the random variable X denote the number of parts that are correctly classified. Determine the probability mass function of X.

Answer 1

The probability mass function (PMF) of a random variable X can be found using the formula P(X = x) = (p)^x * (1-p)^(n-x) * C(n,x), where p is the probability of a correct classification, n is the number of parts inspected, x is the number of parts correctly classified, and C(n,x) is the combinations of n parts taken x at a time.

Step-by-step explanation:

The probability mass function (PMF) of a random variable X can be found by using the formula:

P(X = x) = (p)^x * (1-p)^(n-x) * C(n,x)

Where:

• p = probability of a correct classification (0.98)
• n = number of parts inspected (3)
• x = number of parts correctly classified (0, 1, 2, or 3)
• C(n,x) = combinations of n parts taken x at a time (nCx)

For each value of x (0, 1, 2, 3), plug in the values into the formula to calculate the probability of X taking those values.

Answer 2

P(X=0)=0.000008

P(X=1)=0.00176

P(X=2)=0.057624

P(X=3)=0.941192

Step-by-step explanation:

Probability of correct classification = p = 0.98

Probability of incorrect classification = q = 1 - p = 0.02

The probability of success and failure is the same for all the trials. The trials are independent of each other and the number of trials is fixed i.e. n = 3.

This satisfies all the conditions of a Binomial Experiment. So we can use Binomial experiment to model the probability mass function.

The general formula of a binomial probability is:

`P(X=x)=^(n)C_(x)(p)^(x)q^(n-x)`

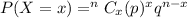
Here x denote the number of successes, which can be {0, 1, 2, 3}. So we need to evaluate the above equation for each value of x to determine the probability Mass function of X, as shown below:

`P(X=0)=^(3)C_(0)(0.98)^(0)(0.02)^(3-0)=0.000008\\\\ P(X=1)=^(3)C_(1)(0.98)^(1)(0.02)^(3-1)=0.001176\\\\ P(X=2)=^(3)C_(2)(0.98)^(2)(0.02)^(3-2)=0.057624\\\\ P(X=3)=^(3)C_(3)(0.98)^(3)(0.02)^(3-3)=0.941192`