Question

A van traveling at a speed of 32.0 mi/h needs a minimum of 42.0 ft to stop. If the same van is traveling 67.0 mi/h, determine its minimum stopping distance (in ft), assuming the same rate of acceleration. ft

Answer 1

Δx= 184.12 ft

Explanation:

The equation you need to use is velocity as a function of displacement.

`v^2= u^2 +2a(\delta x)`

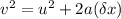
v = the speed at which the car is travelling,

and

v_o is the original speed (in this case zero).

The change in x (displacement) is how far the car travels. You will be solving for a (acceleration).

`32^2= 0^2+ 2a*42`

solving we get

a= 12.19

now put this acceleration value into the second case when v= 67mi/h

`67^2= 0^2 + 2*12.19(change in x)`

⇒Δx= 184.12 ft