Answer:
For a data set with mean = 25 pounds and Standard Deviation = 3 pounds then 95% of the data is between 19 pounds and 31 pounds.
Explanation:
1 ) 68% of the data lies within 1 standard deviation of mean
This means 68% of data lies between:
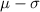 to
to
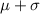
2) 95% of the data lies within 2 standard deviation of mean
This means 95% of data lies between:
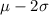 to
to
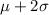
3) 99.7% of the data lies within 3 standard deviation of mean
This means 99.7% of data lies between:
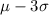 to
to
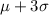
Now,
95% of the data lies within 2 standard deviation of mean :
For Mean =
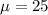
Standard deviation =

So, 95% of data lies between:
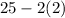 to
to
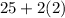
95% of data lies between:
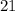 to
to
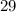
For Mean =
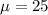
Standard deviation =
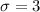
So, 95% of data lies between:
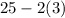 to
to
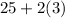
95% of data lies between:
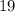 to
to
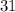
So, Option D is true
For a data set with mean = 25 pounds and Standard Deviation = 3 pounds then 95% of the data is between 19 pounds and 31 pounds.