Answer:
a) About 12%
Explanation:
We need to find the interest rate required to achieve her goal, so we will need to use the interest-compound formula:
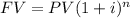
Where:
PV= Present Value
i= interest rate
FV= Future Value
n= number of periods
replacing the data provided:
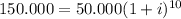
solving for i:
first, divide both sides by 50.000 to simplify the equation:
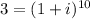
Take
 roots of both sides:
roots of both sides:
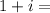 ±
±
![\sqrt[10]{3}](https://img.qammunity.org/2020/formulas/mathematics/high-school/h112f6e67qx6w7aylh6901q15ctsk2brlu.png)
solve for i:
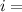 ±
±
![\sqrt[10]{3} -1](https://img.qammunity.org/2020/formulas/mathematics/high-school/aamd5f43bgrs1puaqg2jtqzsoom05fu93y.png)
We get two answers, but we look for a coherent value. So we take the positive one:
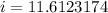 ≈12
≈12