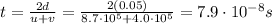Question

An electron is moving in a straight line with a velocity of 4.0×105 m/s. It enters a region 5.0 cm long where it undergoes an acceleration of 6.0×1012m/s2 along the same straight line. (a) What is the electron’s velocity when it emerges from this region? b) How long does the electron take to cross the region?

Answer 1

(a)
`8.7\cdot 10^5 m/s`

We can solve this part of the problem by using the following SUVAT equation:

`v^2-u^2=2ad`

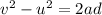
where

v is the final velocity

u is the initial velocity

a is the acceleration

d is the distance through which the electron is accelerated

In this problem,

`u = 4.0\cdot 10^5 m/s\\a = 6.0\cdot 10^(12) m/s^2\\d = 5.0 cm = 0.05 m`

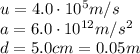
Solving for v,

`v=√(u^2+2ad)=\sqrt{(4.0\cdot 10^5)^2+2(6.0\cdot 10^(12))(0.05)}=8.7\cdot 10^5 m/s`

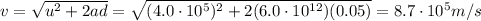
(b)
`7.9\cdot 10^(-8)s`

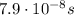
The time needed for the electron to cross the region where it is accelerated can be found by using the following SUVAT equation:

`d=((v+u)/(2))t`

where we have:

d = 5 cm = 0.05 m

`v=8.7\cdot 10^5 m/s`

`u=4.0\cdot 10^5 m/s`

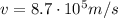
Solving for t, we find:

`t=(2d)/(u+v)=(2(0.05))/(8.7\cdot 10^5+4.0\cdot 10^5)=7.9\cdot 10^(-8)s`