Question

Suppose that in a senior college class of 500500 ​students, it is found that 179179 ​smoke, 228228 drink alcoholic​ beverages, 191191 eat between​ meals, 9999 smoke and drink alcoholic​ beverages, 5959 eat between meals and drink alcoholic​ beverages, 7272 smoke and eat between​ meals, and 3030 engage in all three of these bad health practices. If a member of this senior class is selected at​ random, find the probability that the student​ (a) smokes but does not drink alcoholic​ beverages; (b) eats between meals and drinks alcoholic beverages but does not​ smoke; (c) neither smokes nor eats between meals.

Answer 1

Answer: a) 0.16, b) 0.058, and c) 0.856.

Explanation:

Since we have given that

Number of students = 500

Number of students smoke = 179

Number of students drink alcohol = 228

Number of students eat between meals = 119

Number of students eat between meals and drink alcohol = 59

Number of students eat between meals and smoke = 72

Number of students engage in all three = 30

a) Probability that the student smokes but does not drink alcohol is given by

`P(S-A)=P(S)-P(S\cap A)\\\\P(S-A)=(179)/(500)-(99)/(500)\\\\P(S-A)=(179-99)/(500)\\\\P(S-A)=(80)/(500)\\\\P(S-A)=0.16`

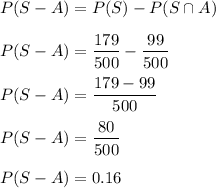
b) eats between meals and drink alcohol but does not smoke.

`P((M\cap A)-S)=P(M\cap A)-P(M\cap S\cap A)\\\\P((M\cap A)-S)=(59)/(500)-(30)/(500)\\\\P((M\cap A)-S)=(59-30)/(500)\\\\P((M\cap A)-S)=(29)/(500)\\\\P((M\cap A)-S)=0.058`

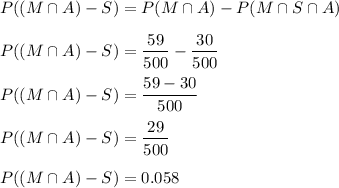
c) neither smokes nor eats between meals.

`P(S'\cap M')=1-P(S\cup M)\\\\P(S'\cap M')=1-(72)/(500)\\\\P(S'\cap M')=(500-72)/(500)\\\\P(S'\cap M')=(428)/(500)=0.856`

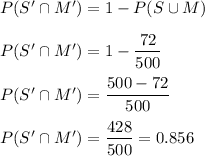
Hence, a) 0.16, b) 0.058, and c) 0.856.