Question

The height of an object thrown upward from the floor of a canyon 106 ft deep, with an initial velocity of 120 ft per second, is given by the equation h=-16x^(2)+120x-106, where h represents the height of the object in feet after x second. How long will it take the object to rise to the height of the canyon wall?

Answer 1

Step-by-step explanation:

The height of an object thrown upward from the floor of a canyon 106 ft deep, with an initial velocity of 120 ft per second. The equation is given by :

`h=-16x^2+120x-106`

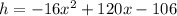
Since, the depth of the canyon is (-106 feet) and the time taken by the object to rise to the height of the canyon wall is calculated as :

h = 0

`-16x^2+120x-106=0`

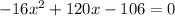
On solving the above quadratic equation,

x₁ = 1.023 seconds

and

x₂ = 6.477 seconds

So, the time taken by the object to rise to the height of the canyon wall is 1.023 seconds (ignoring 6.477 seconds). Hence, this is the required solution.