Question

A vector → A has a magnitude of 56.0 m and points in a direction 30.0° below the negative x axis. A second vector, → B , has a magnitude of 82.0 m and points in a direction 49.0° above the negative x axis. Using the component method of vector addition, find the magnitude of the vector → C = → A + → B .

Answer 1

• The magnitude of the vector
  `\vec{C}` is 107.76 m

Step-by-step explanation:

To find the components of the vectors we can use:

`\vec{A} = | \vec{A} | \ ( \ cos(\theta) \ , \ sin (\theta) \ )`

where
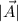`| \vec{A} |` is the magnitude of the vector, and θ is the angle over the positive x axis.

The negative x axis is displaced 180 ° over the positive x axis, so, we can take:

`\vec{A} = 56.0 \ m \ ( \ cos( 180 \° + 30 \°) \ , \ sin (180 \° + 30 \°) \ )`

`\vec{A} = 56.0 \ m \ ( \ cos( 210 \°) \ , \ sin (210 \°) \ )`

`\vec{A} = ( \ -48.497 \ m \ , \ - 28 \ m \ )`

`\vec{B} = 82.0 \ m \ ( \ cos( 180 \° - 49 \°) \ , \ sin (180 \° - 49 \°) \ )`

`\vec{B} = 82.0 \ m \ ( \ cos( 131 \°) \ , \ sin (131 \°) \ )`

`\vec{B} = ( \ -53.797 \ m \ , \ 61.886\ m \ )`

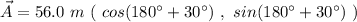
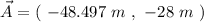
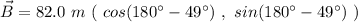
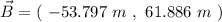
Now, we can perform vector addition. Taking two vectors, the vector addition is performed:

`(a_x,a_y) + (b_x,b_y) = (a_x+b_x,a_y+b_y)`

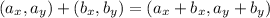
So, for our vectors:

`\vec{C} = ( \ -48.497 \ m \ , \ - 28 \ m \ ) + ( \ -53.797 \ m \ ,  ) = ( \ -48.497 \ m \ -53.797 \ m , \ - 28 \ m \ + \ 61.886\ m \ )`

`\vec{C} = ( \ - 102.294 \ m , \ 33.886 m \ )`

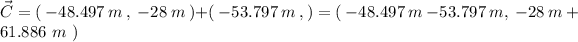
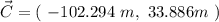
To find the magnitude of this vector, we can use the Pythagorean Theorem

`|\vec{C}| = √(C_x^2 + C_y^2)`

`|\vec{C}| = √((- 102.294 \ m)^2 + (\ 33.886 m \)^2)`

`|\vec{C}| =107.76 m`

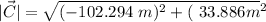
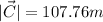
And this is the magnitude we are looking for.