Question

Let C represent the event that a person has cancer. Let D represent the event that a person is diagnosed with cancer. In a certain region of the country it is known from past experience that the probability of selecting an adult over 40 years of age with cancer is 0.08. The probability of a doctor correctly diagnosing a person with cancer as having the disease is P(D | C) = 0.84, and the probability of incorrectly diagnosing a person without cancer as having the disease is P(D | C 0 ) = 0.04. What is the probability that a person diagnosed as having cancer actually has the disease, i.e. find P(C | D)? Round all values to 4 decimals, if needed.

Answer 1

0.6462

Explanation:

Let
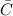`\bar{C}` be the complement of C. We have that P(C)=0.08 because we know from past experience that the probability of selecting an adult over 40 years of age with cancer is 0.08, then the probability of selecting a person over 40 years of age without cancer is

P(
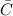`\bar{C}`) =0.92, P(D | C) = 0.84 P(D |
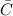`\bar{C}`) = 0.04

Using the Bayes' Formula we have

P(C | D) =
`\frac C)P(C){P(D | C)P(C)+P(D | \bar{C})P(\bar{C})}` =
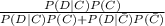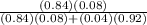`((0.84)(0.08))/((0.84)(0.08)+(0.04)(0.92))` =0.6462

We used the Bayes' Formula because C and
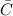`\bar{C}` are mutually exclusive events satisfying
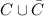`C\cup\bar{C}` = S (S the sample space)