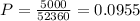Question

Suppose a statistics class contains five freshmen, ten sophomores, ten junior students, and ten senior students. Randomly pick up 4 students from the class to form a study group. What is the probability that the study group contains exactly one freshman, one sophomore, one junior, and one senior?

Answer 1

The probability is 0.0955

Explanation:

The number of ways in which we can select k elements from n elements in which the order is not important is given by combinations and it is calculated as:

`nCk=(n!)/(k!(n-k)!)`

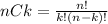
So, the total number of ways in which we can select 4 students from the 35 in the statistics class are:

`35C4=(35!)/(4!(35-4)!)=52,360`

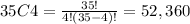
From this, the number of ways in which there are exactly one freshman, one sophomore, one junior and one senior are calculated as:

5C1 * 10C1 * 10C1 * 10C1 = 5,000

Because:

• 5C1 are the number of ways in which we can select one freshman from the 5 that are in the statistics class,
• the first 10C1 are the number of ways in which we can select one sophomore from the 10 that are in the statistics class
• the second 10C1 are the number of ways in which we can select one Junior student from the 10 that are in the statistics class
• the third 10C1 are the number of ways in which we can select one senior student from the 10 that are in the statistics class.

So, the probability is calculated as a division between the number of ways in which there are exactly one freshman, one sophomore, one junior and one senior and the total number of ways in which we can select 4 students from the 35 in the statistics class. This is:

`P=(5000)/(52360)=0.0955`