Answer:
Part a)
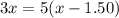
Part b)
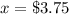
Part c) see the explanation in Part c)
Part d) see the explanation in Part d)
Explanation:
Part a) Write an equation
Let
x -----> represent the cost of one of Tanya's items
y ----> represent the cost of one of Tony's items
we know that
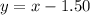
Tanya bought 3 items -----> 3x
Tony bought 5 items -----> 5y----> 5(x-1.50)
If Tanya and Tony paid the same amount of money
then
The cost of three of Tanya's items is equal to the the cost of five of Tony's items
so
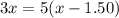
Part b) Solve the equation
we have
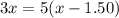
Solve for x
distribute the right side
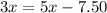
Group terms that contain the same variable
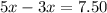
Combine like terms'

Divide by 2 both sides
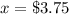
Find the value of y

Part c) Check your solution
substitute the value of x in the originally equation

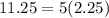
 ----> is verified
----> is verified
Part d) State the solution in complete sentences
we have that
The cost of one of Tanya's items was $3.75
Tanya paid $11.25 for 3 items
The cost of one of Tony's items was $2.25
Tony paid $11.25 for 5 items
Tanya and Tony paid the same amount of money