Question

An engineer designed a valve that will regulate water pressure on an automobile engine. The engineer designed the valve such that it would produce a mean pressure of 5.85.8 pounds/square inch. It is believed that the valve performs above the specifications. The valve was tested on 290290 engines and the mean pressure was 5.95.9 pounds/square inch. Assume the variance is known to be 0.640.64. A level of significance of 0.010.01 will be used. Make a decision to reject or fail to reject the null hypothesis.

Answer 1

Answer with explanation:

Let
`\mu` be the population mean.

By considering the given information , we have

Null hypothesis :
`H_0: \mu=5.85`

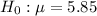
Alternative hypothesis :
`H_0: \mu>5.85`

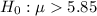
Since alternative hypothesis is right-tailed , so the test is a right-tailed test.

Given : n=290 ;
`\overline{x}=5.95` ;

`\sigma=√(Var)=√(0.64)=0.8`

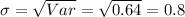
Test statistic:
`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

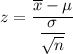
i.e.
`z=(5.95-5.85)/((0.8)/(√(290)))\approx2.13`

By using the standard normal distribution table for z , we have

P-value for right tailed test :
`P(Z>z)=1-P(Z<z)`

`=1-P(z<2.13)=1-0.9834141=0.0165858`

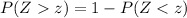
Since , the P-value is greater than the significance level of
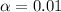`\alpha=0.01` , it means we do not have evidence to reject the null hypothesis.

Hence, we conclude that we do not have enough evidence to support the claim that valve performs above the specifications.