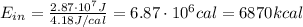Question

In a cycling road race consisting of a flat section and an uphill section, a particular cyclist pedals with an average power of 324 Watts for 5.50 hours on the flat section of the course, and an average power of 418 Watts for 30.0 minutes while climbing the uphill section, which has an average grade of 6%. Potentially useful information: Power = Energy/time; 1 Watt = 1 Joule/sec; 1 kcal = 4186 J

(Note, 1 kcal = 1 food Calorie)

(a) Calculate the average mechanical power output of the cyclist over the whole race.

(b) Given that the human body has an efficiency of 25.0% at converting food energy into mechanical
output, how many kcal of food energy must the cyclist consume to replace the mechanical energy expended during the race?

Answer 1

(a) 332 W

First of all, we need to calculate the energy spent in each part of the race.

The duration of the first part is

`t_1 = 5.50 h \cdot 3600 = 19800 s`

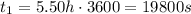
And the average power in this part is

`P_1 = 324 W`

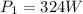
So the energy spent is

`E_1 = P_1 t_1 = (324)(19800)=6.42\cdot 10^6 J`

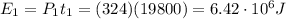
Similarly, the duration of the second part is

`t_2 = 30.0 min \cdot 60 = 1800 s`

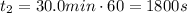
And the average power in this part is

`P_2 = 418 W`

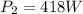
So the energy spent is

`E_2 = P_2 t_2 = (418)(1800)=0.75\cdot 10^6 J`

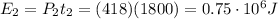
So the total energy consumed is

`E=E_1+E_2=6.42\cdot 10^6 + 0.75\cdot 10^6=7.17\cdot 10^6 J`

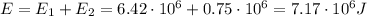
And the total time taken is

`t=t_1+t_2=19800 s +1800 s =21600 s`

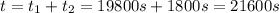
Therefore, the average power output of the cyclist during the whole race is

`P=(E)/(t)=(7.17\cdot 10^6)/(21600)=332 W`

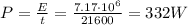
(b) 6870 kcal

We know that the output energy needed by the cyclist to finish the race is

`E_(out)=7.17\cdot 10^6 J`

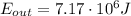
However, the human body converts only 25.0% of the input energy
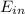`E_(in)` into output energy. So we can write

`(E_(out))/(E_(in))=0.25`

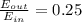
From which we find the food energy that the cyclist must consume:

`E_(in) = (E_(out))/(0.25)=(7.17\cdot 10^6 J)/(0.25)=2.87\cdot 10^7 J`

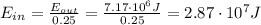
And keeping in mind the conversion between joules and calories:

1 cal = 4.18 J

We find:

`E_(in) = (2.87\cdot 10^7 J)/(4.18 J/cal)=6.87\cdot 10^6 cal = 6870 kcal`