Question

Freight trains can produce only relatively small accelerations. (a) What is the final velocity of a freight train that accelerates at a rate of 0.0500m/s2 for 8.00 min, starting with an initial velocity of 4.00 m/s? (b) If the train can slow down at a rate of 0.550m/s2, how long will it take to come to a stop from this velocity? (c) How far will it travel in each case?

Answer 1

a) 28 m/s b) 50.9s c)i)7680m c)ii) 712m

Step-by-step explanation:

The acceleration is constant in each case, so lets use the ecuations for this kind of motion.

a) For the velocity we have:

`v= v_(0) +at= 4 + 0.05000*480=28(m)/(s)`

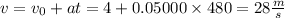
where 480 is the amount of seconds in 8 min

`480 = 60*8`

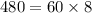
b) In this case we got a 0 velocity, starting with 28 m/s and accelerating at a rate of -0550m/s2 , that means , slowing down.

`0=v= v_(0) +at= 28 - 0.550t`

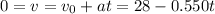
Solving for t:

`t=(28)/(0.55) = 50.9s`

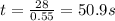
c) Now we can use the equation for the position of a particle with constant acceleration.

`x=x_(0) + v_(0)t+(1)/(2) at^(2)`

In the case of a) we have:

`x=0 + 4*480+(1)/(2)* 0.0500* (480)^(2) =7680m`

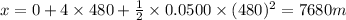
In the case of b) we have

`x=0 + 28*50.9+(1)/(2)* -0.550* (50.9)^(2) =712m`

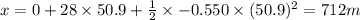
Hope my answer helps you.

Have a nice day!