Question

A eight​-digit code is used to distinguish between different regions. The code uses numbers between 1 and 9​, inclusive. a. How many different codes are available for​ use? (Assume that any eight​-digit number can be used as a​ code.) b. The first three digits of a code for a particular region are 113. If no other region has these first three digits as part of its​ code, how many codes can exist in this​ region?

Answer 1

a.
`9^(8)`

b.
`9^(5)`

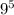
Step-by-step explanation:

Part a

In part a since all the eight digits for the code is to be filled using numbers between 1 and 9. Therefore one digit can have 9 different values, and since there are total 8 digits to be filled.

Therefore total number of different code available for the region will be
`9^(8)` .

Part b

In part b out of eight digits three digits have fixed values i.e. 113. Thus in total there are 5 digits to be filled where each digit can take 9 different value. Therefore, in a region where first three digits of eight digit code are fixed, total number of codes that can exists will be
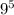`9^(5)`.