Question

The electric field at point P just outside the outer surface of a hollow spherical conductor of inner radius 10 cm and outer radius 20 cm has magnitude 459 N/C and is directed outward. When an unknown point charge Q is introduced into the center of the sphere, the electric field at P is still directed outward but is now 181 N/C. (a) What is the net charge on and enclosed by the outer spherical surface before Q is introduced?

Answer 1

`2.042* 10^(-9)\ C.`

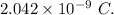
Step-by-step explanation:

Given:

• Electric field just outside the given sphere, E = 459 N/C.
• Inner radius of the shell,
  `\rm r_i` = 10 cm = 0.1 m.
• Outer radius of the shell,
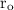  `\rm r_o` = 20 cm = 0.2 m.
• Electric field outside the shell after introducing the charge Q,
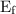  `\rm E_f` = 181 N/C.

Before introducing the charge Q,

Consider a Gaussian sphere of same radius as the outer radius of the shell, concentric with the given shell,

Applying Gauss' law over this surface,

`\oint \vec E \cdot d\vec A = \rm (q)/(\epsilon_o).`

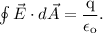
where,

• 
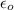  `\epsilon_o` is the electrical permittivity of free space having value
  `9* 10^9\rm \ Nm^2/C^2`.

• 
  `d\vec A` is the surface area element of the sphere, directed along the normal to the plane of the surface.
• 
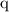  `\rm q` is the net charge enclosed by the Gaussian surface.

The directions of the area element and the electric field, both are directed outward the surface, therefore,
`\vec E \cdot d\vec A = E\ dA`.

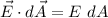The LHS of the equation of the Gauss' law is given as

`\oint \vec E\cdot d\vec A=\oint E\ dA =E\oint dA`

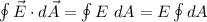
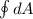`\oint dA` is the surface area of the Gaussian sphere =
`\rm 4\pi r_f^2`

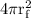
Therefore, using the equation of the Gauss' law,

`\oint \vec E\cdot d\vec A=\rm E\ 4\pi r_f^2=(q)/(\epsilon_o)\\\Rightarrow q =E\ 4\pi r_f^2* \epsilon_o\\=459* 4\pi * (0.2)^2* 8.85* 10^(-12)\\=2.042* 10^(-9)\ C.`

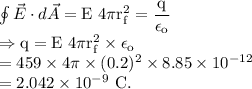
It is the net charge enclosed by the outer surface before Q was introduced.