Question

Two ropes are attached to a heavy box to pull it along the floor. One rope applies a force of 333 newtons (N) in a direction due west; the other applies a force of 590 N in a direction due south. As we will see later in the text, force is a vector quantity. (a) How much force should be applied by a single rope, and (b) in what direction (as a positive angle relative to due west), if it is to accomplish the same effect as the two forces added together?

Answer 1

(a) 677.49 N

(b)
`60.56^\circ`

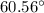
Step-by-step explanation:

Given:

• 
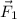  `\vec{F}_1` = force in the first rope = 333 N west =
  `-333\ N\ \hat{i}`

• 
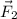  `\vec{F}_2` = force in the second rope = 590 N south =
  `-590\ N\ \hat{j}`

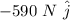
Assume:

• 
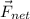  `\vec{F}_(net)` = force in a single rope
• 
  `\theta` = angle with the west direction

We know force as a vector quantity. The two forces acting on the heavy box will have a resultant force whose magnitude and direction will be equivalent to the force required in a single rope that would produce the same effect on the box.

Let us first try to find out the resultant force.

Since the resultant of a force is calculated by the vector addition of all the force vectors.

`\therefore \vec{F}_(net) = \vbec{F}_1+\vec{F}_2\\\Rightarrow  \vec{F}_(net) =(-333\ N\ \hat{i})+(-590\ N\ \hat{j})\\\Rightarrow  \vec{F}_(net) =-333\ N\ \hat{i}-590\ N\ \hat{j}\\`

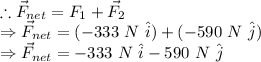
Part (a):

`\textrm{The magnitude of the force in that single rope}=√((-333)^2+(-590)^2)\\\Rightarrow F_(net)= 677.49\ N`

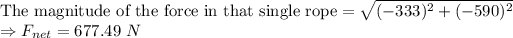
Hence, a force of 677.49 N should be applied by a single rope to do the same effect.

Part (b):

Since the resultant force vector is has its coordinates in the third quadrant of the cartesian vector plane. So, the vector will absolutely make a positive angle with the west direction which is given by:

`\theta = \tan^(-1)((590)/(333))\\\Rightarrow \theta = 60.56^\circ`

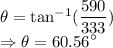
Hence, the rope should be at angle
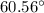`60.56^\circ` south of west.