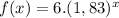Question

Find the equation for the exponential function f (x) = b .aˣ that passes through the points (0,6) and (1,11).

Answer 1

`f(x)=6.(1,83)^(x)`

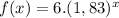
Explanation:

We have two points (0,6) and (1,11) and to find the exponential function that passes through that points we have to substitute them in the equation
`f(x)=b.a^(x)`.

Observation: f(x)=y then
`y=b.a^(x)`

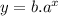
First we are going to replace the point (0,6) in the equation, where x=0 and y=6.

`y=b.a^(x)\\ 6=b.a^(0)`

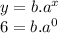
Remember:
`a^(0)=1`

`6=b.a^(0) \\6=b`

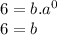
We got the value of b and it's 6. The equation now is:

`y=6.a^(x)`

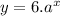
Finally we have to replace the point (1,11),

`y=6.a^(x) \\ 11=6.a^(1) \\ 11=6.a`

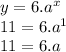
Remember:
`a^(1)=a`

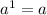
Isolating the variable a:

`11=6.a\\ (11)/(6) =a\\1,83=a`

We have then, a=1.83 and b=6. Replacing a and b in
`f(x)=b.a^(x)`

We obtain:

`f(x)=6.(1,83)^(x)`