Question

What is te factorization of the expression below 9x^2-4y^2

Answer 1

The factorization of the expression
`9 x^(2)-4 y^(2)` is (3x+2y) (3x-2y).

Solution:

In the expression
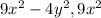`9 x^(2)-4 y^(2), 9 x^(2)` can be written as
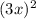`(3 x)^(2)` . Similarly
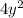`4 y^(2)` can be written as
`(2 y)^(2)`

`9 x^(2)-4 y^(2)=(3 x)^(2)-(2 y)^(2)`

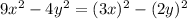
Since both terms
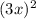`(3 x)^(2)` and
`(2 y)^(2)` are perfect squares, using the difference of squares formula,

`a^(2)-b^(2)=(a+b)(a-b)`

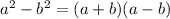
Here a = (3x) and b = (2y)

`(3 x)^(2)-(2 y)^(2)=(3 x+2 y)(3 x-2 y)`

(3x+2y) and (3x-2y) are the factors of
`9 x^(2)-4 y^(2)`