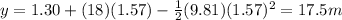Question

Robin would like to shoot an orange in a tree with his bow and arrow. The orange is hanging yf=5.00 m above the ground. On his first try, Robin looses the arrow at ????0=36.0 m/s at an angle of theta=30.0° above the horizontal. The arrow has an initial height of y0=1.30 m, and its tip is x=49.0 m away from the target orange. Treating the arrow as a point projectile and neglecting air resistance, what is the height of the arrow once it has reached the horizontal position x of the orange? Use ????=9.81 m/s2 for the acceleration due to gravity.

Answer 1

17.5 m

Step-by-step explanation:

First of all, we need to find the time the arrow need to cover the horizontal distance between the starting point and the orange, which is

x = 49.0 m

We start by calculating the horizontal component of the arrow's velocity:

`v_x = v_0 cos \theta = (36.0)(cos 30.0^(\circ))=31.2 m/s`

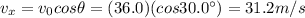
And this horizontal velocity is constant during the entire motion. So, the time taken to reach the horizontal position of the orange is

`t=(x)/(v_f)=(49.0)/(31.2)=1.57 s`

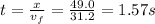
Now we can find the height of the arrow at that time by using the equation for the vertical position:

`y=h+u_y t - (1)/(2)gt^2`

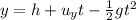
where:

h = 1.30 m is the initial height

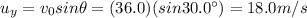`u_y = v_0 sin \theta = (36.0)(sin 30.0^(\circ))=18.0 m/s` is the initial vertical velocity

t = 1.57 s is the time

`g=9.81 m/s^2` is the acceleration of gravity

Substituting into the equation, we find

`y=1.30+(18)(1.57)-(1)/(2)(9.81)(1.57)^2=17.5 m`