Question

How do u do b??????????

Answer 1

the assumption being that the first machine is the one on the left-hand-side and the second is the one on the right-hand-side.

the input goes to the 1st machine and the output of that goes to the 2nd machine.

a)

if she uses and input of 6 on the 2nd one, the result will be 6² - 6 = 30, if we feed that to the 1st one the result will be √( 30 - 5) = √25 = 5, so, simply having the machines swap places will work to get a final output of 5.

b)

clearly we can never get an output of -5 from a square root, however we can from the quadratic one, the 2nd machine/equation.

let's check something, we need a -5 on the 2nd, so

`\bf \underset{final~out put}{\stackrel{y}{-5}}=x^2-6\implies 1=x^2\implies √(1)=x\implies 1=x`

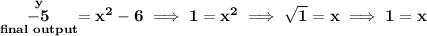
so if we use a "1" as the output on the first machine, we should be able to find out what input we need, let's do that.

`\bf \underset{first~out put}{\stackrel{y}{1}}=√(x-5)\implies 1^2=x-5\implies 1=x-5\implies 6=x`

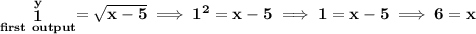
so if we use an input of 6 on the first machine, we should be able to get a -5 as final output from the 2nd machine.

`\bf \stackrel{first~machine}{y=\sqrt{\boxed{6}-5}}\implies y=√(1)\implies y=1 \\\\\\ \stackrel{second~machine}{y = \boxed{1}^2-6}\implies y = 1-6\implies y = -5`