Question

Calculate the present value of the following annuity streams: a. $4,000 received each year for 6 years on the last day of each year if your investments pay 5 percent compounded annually. b. $4,000 received each quarter for 6 years on the last day of each quarter if your investments pay 5 percent compounded quarterly. c. $4,000 received each year for 6 years on the first day of each year if your investments pay 5 percent compounded annually. d. $4,000 received each quarter for 6 years on the first day of each quarter if your investments pay 5 percent compounded quarterly. (For all requirements, do not round intermediate calculations. Round your answers to 2 decimal places. (e.g., 32.16))

Answer 1

Answers:

a) PV 27,207.65

b) PV 111,152.34

c) PV 28,568.03

d) PV 112,541.74

Step-by-step explanation:

The formula for an annuity present value is as follows:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

For each case we will plug the values into and solve:

A)

C 4,000

time 6

rate 0.05

`4000 * (1-(1+0.05)^(-6) )/(0.05) = PV\\`

PV $27,207.6513

B)

C 4,000

time 24 (6 years x4 quearter per year)

rate 0.0125 (5% annual divided by 4 quearter per year)

`4000 * (1-(1+0.0125)^(-24) )/(0.0125) = PV\\`

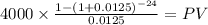
PV $111,152.3361

C) same as A) but being an annuity-due, whch means the payment are made at the beginning of the period:

ordinary annuity x (1+r) = annuity-due

$27,207.6513 x 1.05 = $28,568.0338

D) same procedure as C:

ordinary annuity x (1+r) = annuity-due

$111,152.3361 x 1.05 = $112,541.7403