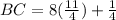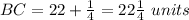Answer:
Part 1) x=5, AB=65 units, BC=30 units
Part 2) x=8, AB=16 units, BC=32 units
Part 3) x=9, AB=4.1 units, BC=4.5 units
Part 4) x=2 3/4, AB=16 1/2 units, BC=22 1/4 units
Explanation:
The complete question in the attached figure
we have that
Point B is between A and C on segment AC
we know that
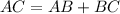 -----> equation A (by addition segment postulate)
-----> equation A (by addition segment postulate)
Part 1) we have
AC = 95, AB = 15x - 10, BC = 5x + 5
substitute the given values in equation A and solve for x
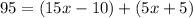
Combine like terms in the right side

Adds 5 both sides
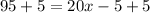
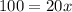
Divide by 20 both sides


Rewrite

Find the value of AB
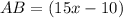
substitute the value of x

Find the value of BC
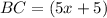
substitute the value of x
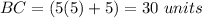
Part 2) we have
AC = 8x - 16, AB = 3x - 8, BC = 4x
substitute the given values in equation A and solve for x
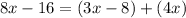
Combine like terms in the right side

Adds 16 both sides
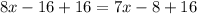
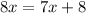
Subtract 7x both sides
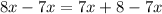
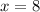
Find the value of AB
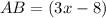
substitute the value of x
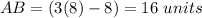
Find the value of BC
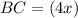
substitute the value of x
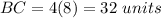
Part 3) we have
AC = x - 0.4, AB = x - 4.9, BC = 0.5x
substitute the given values in equation A and solve for x
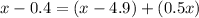
Combine like terms in the right side
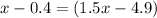
Adds 4.9 both sides

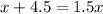
Subtract x both sides
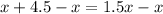
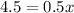
Divide by 0.5 both sides
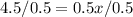
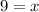
Rewrite
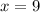
Find the value of AB

substitute the value of x
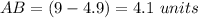
Find the value of BC
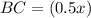
substitute the value of x
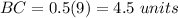
Part 4) we have
AC = 38 3/4, AB = 6x, BC = 8x + 1/4
substitute the given values in equation A and solve for x

Convert mixed number to an improper fraction
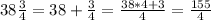
substitute
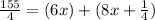
Multiply by 4 both sides to remove the fraction
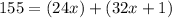
Combine like terms in the right side
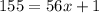
Subtract 1 both sides
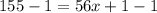
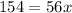
Divide by 56 both sides
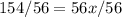
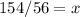
Rewrite
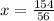
Simplify
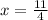
Rewrite x as mixed number
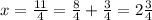
Find the value of AB
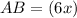
substitute the value of x
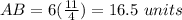
Rewrite AB as mixed number
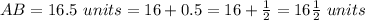
Find the value of BC
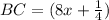
substitute the value of x