Answer with explanation:
Binomial probability formula to find the probability of getting success in x trials is given by :-
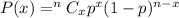 , where n is the sample size , p is the proportion of getting success in each trial. (1)
, where n is the sample size , p is the proportion of getting success in each trial. (1)
Given : A boxcar contains six complex electronic systems. Two of the six are to be randomly selected for thorough testing and then classified as defective or not defective.
i.e. n= 2
a) If three of the six systems are actually defective.
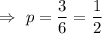
Then, the probability that at least one of the two systems tested will be defective will be :_
![P(x\geq1)=1-P(x=0)\\\\=1-^(2)C_(0)((1)/(2))^0((1)/(2))^(2) \ \ \text{[By using formula (1)]}\\\\=1-((1)/(2))^2\ \ \because\ ^nC_0=1\\\\=1-(1)/(4)=(3)/(4)](https://img.qammunity.org/2020/formulas/mathematics/college/55h9dreifkww8zffschmyj9n6ubemmijqy.png)
Hence, the probability that at least one of the two systems tested will be defective =

b) If four of the six systems are actually defective.
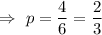
Then, the probability that at least one of the two systems tested will be defective will be :_
![P(x\geq1)=1-P(x=0)\\\\=1-^(2)C_(0)((2)/(3))^0(1-(2)/(3))^(2) \ \ \text{[By using formula (1)]}\\\\=1-((1)/(3))^2\ \ \because\ ^nC_0=1\\\\=1-(1)/(9)=(8)/(9)](https://img.qammunity.org/2020/formulas/mathematics/college/m7jumi9k4mvh6i7x3zj9m4hseedu4b1x21.png)
Hence, the probability that at least one of the two systems tested will be defective =

The probability that both are defective :
![P(x=2)=^(2)C_(2)((2)/(3))^2(1-(2)/(3))^(0) \ \ \text{[By using formula (1)]}\\\\=((2)/(3))^2\ \ \because\ ^nC_n=1\\\\=(4)/(9)](https://img.qammunity.org/2020/formulas/mathematics/college/tnv52gbznroc3yqjsexz1ws1pijmnzmkoj.png)
Hence, the probability that both are defective =
