Question

Does anyone know how to solve this math equation?

(Solve by Elimination, Substitution, or Matrices)
Thank you !!!

Answer 1

x = 8; y = -6

Explanation:

We have a system of equations.

`(3(x - 2))/(2) - (y - 2)/(4) = 11`

`(2(x + 2))/(5) - (y)/(3) = 6`

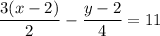
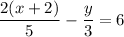
First, let's multiply both sides of each equation by the LCM of both denominators of that equation to eliminate all denominators.

First equation:

`8 * (3(x - 2))/(2) - 8 * (y - 2)/(4) = 8 * 11`

`12(x - 2) - 2(y - 2) = 88`

`12x - 24 - 2y + 4 = 88`

`12x - 2y = 108`

`6x - y = 54`

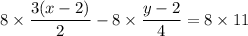
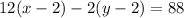
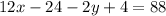
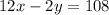
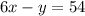
The equation above is the simplified first equation.

Second equation:

`(2(x + 2))/(5) - (y)/(3) = 6`

`15 * (2(x + 2))/(5) - 15 * (y)/(3) = 15 * 6`

`6(x + 2) - 5y = 90`

`6x + 12 - 5y = 90`

`6x - 5y = 78`

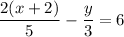
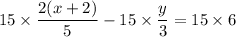
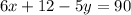
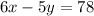
The equation above is the simplified second equation.

The simplified system of equations is:

`6x - y = 54`

`6x - 5y = 78`

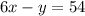
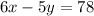
The x term of both equations is 6x. If we multiply both sides of the second equation by -1 to get a first term of -6x, then when it is added to 6x, the x terms are eliminated.

Now we rewrite the first simplified equation as it is. Below it, we write the second equation multiplied by -1 on both sides. Then we add the equations.

`6x - y = 54`

`-6x + 5y = -78`

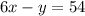
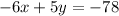
Add the equations to get:

`4y = -24`

`y = -6`

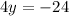
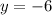
Now we substitute -6 for y in the first simplified equation and solve for x.

`6x - y = 54`

`6x - (-6) = 54`

`6x + 6 = 54`

`6x = 48`

`x = 8`

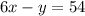
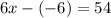
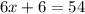
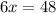
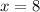
Solution: x = 8; y = -6