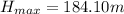Answer: 184.10 m
Step-by-step explanation:
In order to solve this problem, we have to divide it into two parts:
a) When the rocket is moving with an acceleration
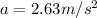
b) When the rocket is moving with an acceleration

So, for part a we have the following data:
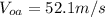 is the initial speed from ground
is the initial speed from ground
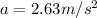 is the upward acceleration due to the rocket's engines
is the upward acceleration due to the rocket's engines
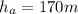 is the height the rocket reaches with this acceleration
is the height the rocket reaches with this acceleration
We have to find the "final speed"
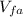 the rocket has when it reaches
the rocket has when it reaches
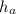 :
:
 (1)
(1)
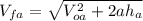 (2)
(2)
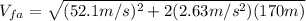 (3)
(3)
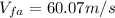 (4)
(4)
Then we have to find the time it took to the rocket to reach this velocity
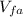 with the following equation:
with the following equation:
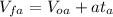 (5)
(5)
 (6)
(6)
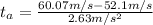 (7)
(7)
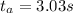 (8)
(8)
Now we move to part b:
At this point the acceleration is the acceleration due gravity (
 ) and the final velocity
) and the final velocity
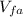 we calculated in equation (4) part a, is now the initial velocity
we calculated in equation (4) part a, is now the initial velocity
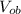 in this part b:
in this part b:
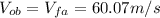
On the other hand, it is known that in projectile motion (as this situation) the maximum height
 is when the velocity of the rocket is zero (
is when the velocity of the rocket is zero (
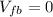 ).
).
So, we will use equation (1) again but with this new data:
 (9)
(9)
Isolating
 :
:
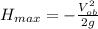 (10)
(10)
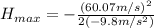 (11)
(11)
Finally: