Answer:
A.
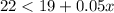
B. If a customer makes more than 60 monthly calls, then Plan 1 is more economical
Explanation:
Let x be the number of calls, y - total cost per month
Plan 1: $22 per month for unlimited calls, then
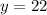
Plan 2: $19 per month plus $0.05 per call ($0.05x for x calls). Then
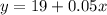
A. If Plan 1 is more economical than Plan 2, then the total cost in Plan 1 is less than the total cost in Plan 2. Thus,
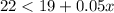
B. Solve this inequality:
![22<19+0.05x\\ \\0.05x+19>22\\ \\0.05x+19-19>22-19\\ \\0.05x>3\\ \\5x>300\ [\text{ Multiplied by 100}]\\ \\x>60\ [\text{ Divided by 5}]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6n6iv7jvvvey4bbbfwym4jv5rd5l32ep5a.png)
Meaning: If a customer makes more than 60 monthly calls, then Plan 1 is more economical