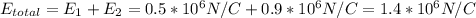Question

A +5.0-μC point charge is placed at the 0 cm mark of a meter stick and a -4.0-μC charge is placed at the 50 cm mark. What is the net electric field at the 30 cm mark? (k = 1/4πε0 = 8.99 × 109 N • m2/C2) A +5.0-μC point charge is placed at the 0 cm mark of a meter stick and a -4.0-μC charge is placed at the 50 cm mark. What is the net electric field at the 30 cm mark? (k = 1/4πε0 = 8.99 × 109 N • m2/C2) 4.0 × 105 N/C 1.4 × 106 N/C 9.0 × 105 N/C 5.0 × 105 N/C

Answer 1

1.4 *10^6 N/C

Step-by-step explanation:

The electric field caused by a charge at a certain point is given by the equation:

`E = k (q)/(r) \^r`

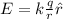
where k is the Coulomb constant equal to 8.99 *10^9 Nm^2/C^2, q the charge of the particle in coulombs, r is the distance from the point to the charge in meters.

`\^r` is the unitary vector that goes from the charge to the point. This vector will give us the direction of the Electric Field vector.

The unitary vector of the +5.0-μC charge will go to the right (+i), as the point is to the right of the charge. Then, the electric field caused by the charge will be:

`E_1 = k (q)/(r^2) \^r = 8.99*10^9 Nm^2/C^2 (5.0 *10^(-6)C)/((0.3m - 0m)^2)(+\^i) =  +0.5*10^6 N/C`

The unitary vector of the -4.0-μC charge will go to the left (-i), as the point is to the left of the charge. Then, the electric field caused by the charge will be:

`E_2 = k (q)/(r^2) \^r = 8.99*10^9 Nm^2/C^2 (-4.0 *10^(-6)C)/((0.5m - 0.3m)^2)(-\^i) =  +0.9*10^6 N/C`

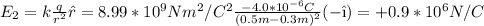
The electric field at the 30 cm mark will be the addition of both electric field:

`E_(total) = E_1 +E_2 = 0.5 *10^6 N/C + 0.9*10^6 N/C = 1.4 *10^6 N/C`