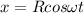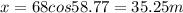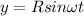Answer:
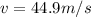
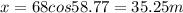

Step-by-step explanation:
As we know that car drives at constant speed along circular path then we will have its position vector given as

now if we differentiate is with respect to time then it will give as instantaneous velocity
so we have

now again its differentiation with respect to time will give us acceleration

now if we compare it with given value of acceleration
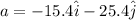
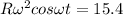
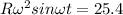
divide both equations then we will have
[tec]tan\omega t = 1.65[/tex]
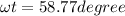
Now we have
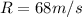
so we can solve it for
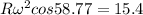

so speed of the car is given as
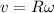
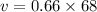
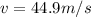
now we have coordinates of car given as