Question

The large sphere has a diameter of 12 feet. A large sphere has a diameter of 12 feet. A smaller sphere with a radius of 3 feet is cut out of the center of the larger sphere. The shaded area if the remaining area of the larger sphere. What is the volume of the shaded figure? Express the answer in terms of π. 252π ft3 261π ft3 288π ft3 324π ft3

Answer 1

252π feet³

Explanation:

Answer 2

The volume of the shaded figure is 252π feet³ ⇒ 1st answer

Explanation:

* Lets revise how to find the volume of the sphere

- The volume of any sphere is
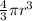`(4)/(3)\pi r^(3)`, where

r is the radius of the sphere

- There is a large sphere of diameter 12 feet

- The diameter of the sphere is twice its radius

∵ The length of the diameter is 12 feet

∴ The length of the radius =
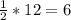`(1)/(2)*12=6` feet

- There is a smaller sphere with a radius of 3 feet

- The smaller sphere is cut out of the center of the larger sphere

- The volume of the shaded part is the difference between the

volumes of the larger sphere and the smaller sphere

* Lets find the volume of each sphere

- The volume of the larger sphere:

V larger =
`(4)/(3)\pi (6)^(3)` = 288π feet³

- The volume of the smaller sphere:

V smaller =
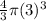`(4)/(3)\pi (3)^(3)` = 36π feet³

∴ The volume of the shaded figure = 288π - 36π = 252π feet³

* The volume of the shaded figure is 252π feet³