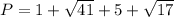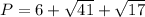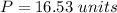Question

Find the perimeter of quadrilateral PQRS with the vertices P(2,4), Q(2,3), R(-2,-2), and S(-2,3).

Answer 1

`P=16.53\ units`

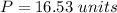
Explanation:

we know that

The perimeter of quadrilateral PQRS is equal to the sum of its four length sides

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

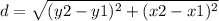
we have

the vertices P(2,4), Q(2,3), R(-2,-2), and S(-2,3)

step 1

Find the distance PQ

P(2,4), Q(2,3)

substitute in the formula

`d=\sqrt{(3-4)^(2)+(2-2)^(2)}`

`d=\sqrt{(-1)^(2)+(0)^(2)}`

`d=√(1)`

`dPQ=1\ unit`

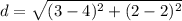
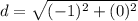
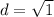
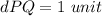
step 2

Find the distance QR

Q(2,3), R(-2,-2)

substitute in the formula

`d=\sqrt{(-2-3)^(2)+(-2-2)^(2)}`

`d=\sqrt{(-5)^(2)+(-4)^(2)}`

`dQR=√(41)\ units`

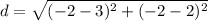
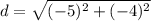
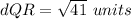
step 3

Find the distance RS

R(-2,-2), and S(-2,3)

substitute in the formula

`d=\sqrt{(3+2)^(2)+(-2+2)^(2)}`

`d=\sqrt{(5)^(2)+(0)^(2)}`

`dRS=5\ units`

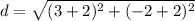
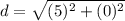
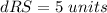
step 4

Find the distance PS

P(2,4), S(-2,3)

substitute in the formula

`d=\sqrt{(3-4)^(2)+(-2-2)^(2)}`

`d=\sqrt{(-1)^(2)+(-4)^(2)}`

`dPS=√(17)\ units`

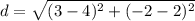
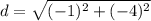
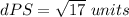
step 5

Find the perimeter

`P=PQ+QR+RS+PS`

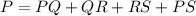
substitute the values

`P=1+√(41)+5+√(17)`

`P=6+√(41)+√(17)`

`P=16.53\ units`