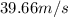Question

Two subway stops are separated by 1210 m. If a subway train accelerates at 1.30 m/s2 from rest through the first half of the distance and decelerates at -1.30 m/s2 through the second half, what are (a) its travel time and (b) its maximum speed?

Answer 1

Part 1) Time of travel equals 61 seconds

Part 2) Maximum speed equals 39.66 m/s.

Step-by-step explanation:

The final speed of the train when it completes half of it's journey is given by third equation of kinematics as

`v^(2)=u^2+2as`

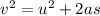
where

'v' is the final speed

'u' is initial speed

'a' is acceleration of the body

's' is the distance covered

Applying the given values we get

`v^2=0+2* 1.30* (1210)/(2)\\\\v^(2)=1573\\\\\therefore v=39.66m/s`

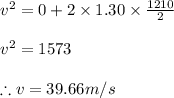
Now the time taken to attain the above velocity can be calculated by the first equation of kinematics as

`v=u+at\\\\v=0+1.30* t\\\\\therefore t=(39.66)/(1.30)=30.51seconds`

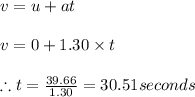
Since the deceleration is same as acceleration hence the time to stop in the same distance shall be equal to the time taken to accelerate the first half of distance

Thus total time of journey equals
`T=2* 30.51\approx61seconds`

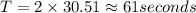
Part b)

the maximum speed is reached at the point when the train ends it's acceleration thus the maximum speed reached by the train equals
`39.66m/s`