Answer:
2400 in the section of cost $60 for each ticket
800 in the section of cost $90 for each ticket
400 in the section of cost $100 for each ticket
Step-by-step explanation:-
- A theater owner wants to divide a 3600 seat theater into 3 sections
- The tickets of the sections costing $60, $90, and $100
- He wants to have twice as many $ 60 tickets as the sum of the
other tickets
- He wants to earn $256,000 from a full theater
- Assume that x represents the number of tickets cost $60, y represents
the number of tickets cost $90, and z represents the number of tickets
cost $100
∵ The total number of tickets = 3600
∴ x + y + z = 3600 ⇒ (1)
∵ The number of $60 tickets is twice the sum of the other tickets
∴ x = 2(y + z)
- divide both sides by 2
∴
 ⇒ (2)
⇒ (2)
- Substitute equation (2) in equation (1)
∴
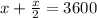
∴ 1.5x = 3600
- Divide both sides by 1.5
∴ x = 2400
∵ He wants to earn $256,000 from a full theater
∵ x cost $60 each
∵ y cost $90 each
∵ z cost $100 each
∴ 60x + 90y + 100z = 256000
∴ 60(2400) + 90y + 100z = 256000
∴ 144000 +90y + 100z = 256000
- Subtract both sides by 144000
∴ 90y + 100z = 112000
- Divide both sides by 10 to simplify it
∴ 9y + 10z = 11200 ⇒ (3)
- Substitute value of x in equation (2)
∴
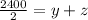
∴ 1200 = y + z
∴ y + z = 1200 ⇒ (4)
- Solve equations (3) , (4) to find y and z
- Multiply equation (4) by -10 to eliminate z
∴ -10y - 10z = -12000 ⇒ (5)
- Add equations (3) and (5)
∴ -y = -800
- Multiply both sides by -1
∴ y = 800
- Substitute the value of y in equation (4) to find z
∴ 800 + z = 1200
- subtract both sides by 800
∴ z = 400
∴ The number of seats in each section:
2400 in the section of cost $60 for each ticket
800 in the section of cost $90 for each ticket
400 in the section of cost $100 for each ticket