Answer:
a)
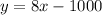
b)
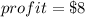
c) They'd have lost $1000 if they had sold no calendars.
Explanation:
a) The equation of the line in Slope-Intercept form is:

Where "m" is the slope and "b" is the y-intercept.
In this case we know that "y" represents the profit of loss and "x" the number of calendars sold.
Then, according to the exercise, the line passes through these two points:
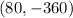 and
and
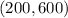
Then, we can find the slope of the line with the formula

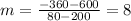
Now, we can substitute the slope and one of those points into
 and solve for "b":
and solve for "b":

Then, subtituting values, we get that the equation that describes the relation between the profit of loss and the number of calendars sold, is:
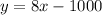
b) The slope of the line is the profit they made from selling each calendar
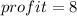
c) The y-intercept is the amount they would have lost if they had sold no calendars:

They'd have lost $1000 if they had sold no calendars.