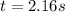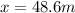Answer:
The car moved a distance
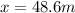 .
.
Step-by-step explanation:
First we need to know: How much time will the tomato spend in the air?
From Kinematics:

where
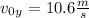 and
and
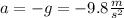 is gravity's acceleration.
is gravity's acceleration.
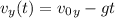
When the tomato touches the car again,
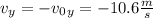
Then, we have:
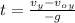 ⇒
⇒
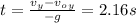
Also from Kinematics we have:
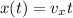
Which is very simple because we can take initial position 0 and there's no acceleration in the x direction. And
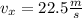
So, taking