Question

A plane leaves the airport in Galisteo and flies 170 km at 68.0° east of north; then it changes direction to fly 230 km at 36.0° south of east, after which it makes an immediate emergency landing in a pasture. When the airport sends out a rescue crew, in which direction and how far should this crew fly to go directly to this plane?

Answer 1

The direction will be
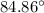`84.86^\circ` and the distance 250.75km.

Step-by-step explanation:

Let's say A is the displacement vector which represents the first 170km and B the one for the next 230km. Then the components of these vector will be:

`A_x=170cos(68^(\circ))\\ A_y=170sin(68^\circ)\\\\B_x=230cos(-36^\circ)\\B_y=230sin(-36^\circ)`

The vector which point from the origin to the final position of the plane will be R=A+B. We sum components on x and y independetly (vector property):

`R_x=A_x+B_x=170cos(68^(\circ))+230cos(-36^\circ)=63.68km+186.07km=249.75km`

`R_y=A_y+B_y=170sin(68^\circ)+230sin(-36^\circ)=157.62km-135.19km=22.43km`

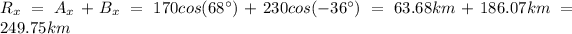
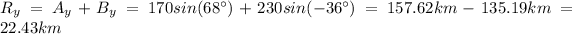
If
`\theta` is the direction of R then:

`tan(\theta )=(R_x)/(R_y)` ⇒
`\theta = arctan((R_x)/(R_y))` ⇒
`\theta = 84.86^\circ`.

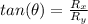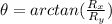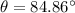The distance will be given by the magnitud of the vector R:

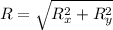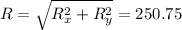`R=√(R_x^2 + R_y^2)` ⇒
`R=√(R_x^2 + R_y^2) = 250.75`.