Question

An electron is released from rest at the negative plate of a parallel plate capacitor. The charge per unit area on each plate is σ = 1.69E-7 C/m2, and the plates are separated by a distance of 1.75E-2 m. How fast is the electron moving just before it reaches the positive plate?

Answer 1

`v=1.08* 10^7\ m/s`

Step-by-step explanation:

Initial speed of the electron, u = 0

The charge per unit area of each plate,
`(Q)/(A)=1.69* 10^(-7)\ C/m^2`

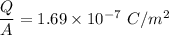
Separation between the plates,
`d=1.75* 10^(-2)\ m`

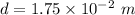
An electron is released from rest, u = 0

Using equation of kinematics,

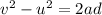`v^2-u^2=2ad`..........(1)

Acceleration of the electron in electric field,
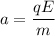`a=(qE)/(m)`............(2)

Electric field,
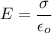`E=(\sigma)/(\epsilon_o)`............(3)

From equation (1), (2) and (3) :

`v=\sqrt{(2q\sigma d)/(m\epsilon_o)}`

`v=\sqrt{(2* 1.6* 10^(-19)* 1.69* 10^(-7)* 1.75* 10^(-2))/(9.1* 10^(-31)* 8.85* 10^(-12))}`

v = 10840393.1799 m/s

or

`v=1.08* 10^7\ m/s`

So, the electron is moving with a speed of
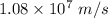`1.08* 10^7\ m/s` before it reaches the positive plate. Hence, this is the required solution.