Answer:
The following equation has:
Unique solution (one solution i.e. (4,1) )
Explanation:
The system of equation is given by:
y= -x + 5-----------(1)
and y= x - 3------------(2)
Now, on substituting the value of y from equation (1) into equation (2) we have:
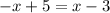
On adding x on both the sides of the equation we have:
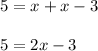
on adding 3 on both the sides of the equation we have:

Now, on putting the value of x into equation (2) we have:

Hence, the solution is unique (one solution )
Also, the point of intersection of the graph of two equations is solution to the system of equations.