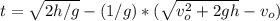Answer:
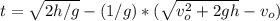
Step-by-step explanation:
First person:
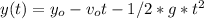
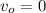 the rock is dropped
the rock is dropped
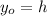
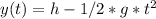
after t1 seconds it hit the ground, y(t)=0
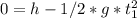
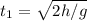
Second person:
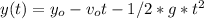
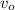 the rock has a initial downward speed
the rock has a initial downward speed
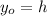
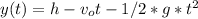
after t2 seconds it hit the ground, y(t)=0
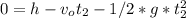
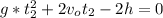
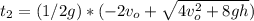
the time t when the second person throws the rock after the first person release the rock is:
t=t1-t2